Треугольник
Треуго́льник — многоугольник, имеющий 3 вершины и 3 стороны; часть плоскости, ограниченная тремя точками, не лежащими на одной прямой, и тремя отрезками, попарно соединяющими эти точки.
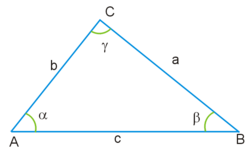
Вершины треугольника обычно обозначаются заглавными латинскими буквами (A, B, C), величины углов при соответственных вершинах — греческими буквами (α,β,γ), а длины противоположных сторон — прописными латинскими буквами (a, b, c).
Неравенство треугольника[править | править код]
Стороны треугольника нельзя задавать произвольно; все три стороны треугольника не больше суммы двух других. В случае равенства треугольник называется вырожденным, в дальнейшем предполагаем невырожденный случай.
Признаки равенства треугольников[править | править код]
Треугольник однозначно (с точностью до конгруэнтности) можно определить по следующим тройкам основных элементов:
- a, b, c (равенство по трём сторонам);
- a, b, γ (равенство по двум сторонам и углу между ними);
- a, β, γ (равенство по стороне и двум прилежащим углам).
В плоскости Лобачевского добавляется признак равенства по трём углам.
Отрезки и окружности, связанные с треугольником[править | править код]
Окружность, касающаяся всех трех сторон треугольника, называется его вписанной окружностью. Она единственна. Окружность, проходящая через все три вершины треугольника, называется его описанной окружностью. Описанная окружность также единственна.
Медианой треугольника, проведенной из данной вершины, называется отрезок, соединяющий эту вершину с серединой противолежащей стороны. Все три медианы треугольника пересекаются в одной точке. Эта точка пересечения называется центроидом или центром тяжести треугольника. Последнее название связано с тем, что у треугольника, сделанного из однородного материала, центр тяжести находится в точке пересечения медиан. Центроид делит каждую медиану в отношении 1:2, считая от основания медианы.
Перпендикуляр, опущенный из вершины треугольника на противоположную сторону или ее продолжение, называется высотой треугольника. Три высоты треугольника пересекаются в одной точке, называемой ортоцентром треугольника.
Биссектрисой треугольника, проведенной из данной вершины, называют отрезок, соединяющий эту вершину с точкой на противоположной стороне и делящий угол при данной вершине пополам. Биссектрисы треугольника пересекаются в одной точке, и эта точка совпадает с центром вписанной окружности.
В равнобедренном треугольнике биссектриса, медиана и высота, проведенные к основанию, совпадают. Верно и обратное: если биссектриса, медиана и высота, проведенные из одной вершины, совпадают, то треугольник равнобедренный. Также в равнобедренном треугольнике биссектрисы, высоты и медианы, проведённые из основания, равны. Если треугольник разносторонний, то для любой его вершины биссектриса, проведенная из нее, лежит между медианой и высотой, проведенными из той же вершины.
Серединные перпендикуляры к сторонам треугольника также пересекаются в одной точке, которая совпадает с центром описанной окружности.
Вневписанной окружностью называется окружность, касающаяся одной стороны треугольника и продолжения двух других сторон.
Середины трех сторон треугольника, основания трех его высот и середины трех отрезков, соединяющих его вершины с ортоцентром, лежат на одной окружности, называемой окружностью девяти точек.
В любом треугольнике центр тяжести, ортоцентр, центр описанной окружности и центр окружности девяти точек лежат на одной прямой, называемой прямой Эйлера.
Соотношения в треугольнике[править | править код]
Если известны три величины, указанные выше, то остальные можно найти по следующим формулам:
Теорема синусов[править | править код]
(Из теоремы следует, что если a < b < c, то α < β < γ)
Теорема косинусов[править | править код]
- c2 = a2 + b2 — 2ab cos γ
(Является обобщением теоремы Пифагора)
Теорема о сумме углов треугольника[править | править код]
- α + β + γ = 180° (π)
Прочие соотношения[править | править код]
Метрические соотношения в треугольнике приведены для треугольника :
Где:
— соответственно биссектрисы углов , и ,
— отрезки, на которые биссектриса делит сторону ,
— медианы, проведенные соответственно к сторонам , и ,
— высоты, опущенные соответственно на стороны , и ,
— радиус вписанной окружности,
— радиус описанной окружности,
- координаты центра описанной окружности ,
— полупериметр,
— площадь,
— расстояние между центрами вписанной и описанной окружностей.
Площадь треугольника[править | править код]
- , так как , то:
- — формула Герона
- в данной формуле следует обратить внимание на обход вершин, если идти по часовой стрелке, то получится та же площадь, но с отрицательным знаком
- — для прямоугольного треугольника
Где:
— высота, проведённая на сторону ,
— полупериметр,
— радиус вписанной окружности,
— радиус вневписанной окружности, касающейся стороны ,
— радиус описанной окружности,
— координаты вершин треугольника.
Типы треугольников[править | править код]
| Виды треугольников | ||
|---|---|---|
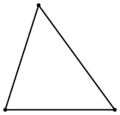 Остроугольный |
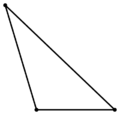 Тупоугольный |
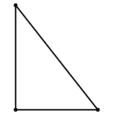 Прямоугольный |
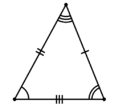 Разносторонний |
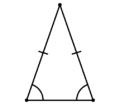 Равнобедренный |
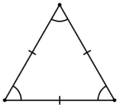 Равносторонний |
По величине углов[править | править код]
Поскольку сумма углов треугольника равна 180°, то не менее двух углов в треугольнике должны быть острыми (меньшими 90°). Выделяют следующие виды треугольников:
- Если все углы треугольника острые, то треугольник называется остроугольным;
- Если один из углов треугольника тупой (больше 90°), то треугольник называется тупоугольным;
- Если один из углов треугольника прямой (равен 90°), то треугольник называется прямоугольным. Две стороны, образующие прямой угол, называются катетами, а сторона, противолежащая прямому углу, называется гипотенузой.
По числу равных сторон[править | править код]
- Разносторонним называется треугольник, у которого длины трех сторон попарно различны.
- Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, третья сторона называется основанием. В равнобедреном треугольнике углы при основании равны. Высота, медиана и биссектриса равнобедренного треугольника, опущенные на основание, совпадают.
- Равносторонним называется треугольник, у которого все три стороны равны. В равностороннем треугольнике все углы равны 60°, а центры вписанной и описанной окружностей совпадают.
См. также[править | править код]
- Теорема о сумме углов треугольника
- Теорема синусов
- Теорема косинусов
- Формула Герона
- Замечательные точки треугольника
- Средняя линия треугольника
- Теорема Чевы
- Треугольник Рёло
- Штрихкод треугольника